大型ヘリカル装置(LHD)中のプラズマの複雑な挙動を調べるため、圧縮性を有する電磁流体力学(MHD)方程式の直接数値計算(DNS)を行っている。 計算手法は主に差分法とルンゲ・クッタ・ジル法の組み合わせである。
この研究については、Phys. Plasmas, IAEA 核融合会議プロシーディングスなどを参照。
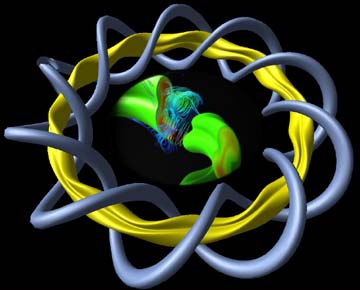
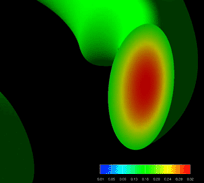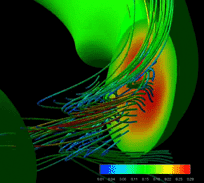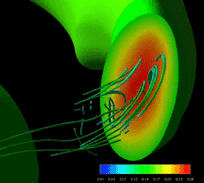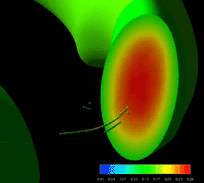


Direct numerical simulation of compressible Magnetohydrodynamics
in the
Large Helical Device
Complex behaviors of plasmas in the Lharge Helical Device (LHD) are
investigated
by means of direct numerical simulations (DNS) of compressible
Magnetohydrodynamics
(MHD) eqautions. The equations are discretized by the compact finite
diference scheme (now 8th order) and marched in the time direction by
Runge-Kutta-Gill scheme.
In our simulations, toroidal (parallel to the magnetic field lines)
flows are strongly excited.
The flows are initially excited as a part of the linear eigen-mode.
While the perpendicular flows are scattered and/or damped through the
nonlinear saturation and the relaxations after it, the parallel flows
appear to have quite longer life time.
After the saturations, the plasma tends to go back to (relatively)
well-confined state, as is seen in the movie on this web page.
In the relaxation stage, the internal energy (pressure) has been
convereted into the toroidal kinetic energy and no free energy to
drive next instability.
Consequently, the plasma stabilize itself not only by nonlinear
deformations of the pressure but also by releasing the free energy
into the parallel direction.
In the course of the linear evolutions, the compressibility also
contributes significantly to suppress the growth rates of the unstable
modes.
In our simulations, it is estimated that the compressible terms have
about 2/3 times amplitude of the linear driving terms and works to
suppress the linear growth.
From the numerical results, the compressibility
Confinement in LHD may be